1/3×3 = 1 のはずなのに 0.3333…×3 = 0.9999… のパラドックス  緋山: YouTube動画や webの解説サイトで色々調べたのですが 整数(1)と少数(0.99999…)では表現が違うことぐらいしか 分かりません 不思議です 教授: 0.999999…ですが、これは1に等しいです 初項がa で公比が r の等比数列 a, ar, ar^2, ar^3, … これの和を考えてみます n項目までの和 Sn を計算すると Sn = a + ar + ar^2 + … + ar^(n-1) (1) となります 緋山: n項目までの和なのに なぜ最後が n-1 なのですか? 教授: 和の最初の項は a=ar^0 です 2番目の項は ar = ar^1, 3番目の項は ar^2, … なので n 番目の項は ar^(n-1) です 続けます Sn = a + ar + ar^2 + … + ar^(n-1) (1) となります これを r 倍すると r × Sn = ar + ar^2 + … + ar^(n-1) + ar^n (2) となります 緋山: (2)を説明してもらえますか? 教授: a に r をかけると ar ar に r をかけると ar^2 ar^2 に r をかけると ar^3 … ar^(n-2) に r をかけると ar^(n-1) ar^(n-1) に r をかけると ar^n なので Sn = a + ar + ar^2 + … + ar^(n-2) + ar^(n-1) ならば r × Sn = ar + ar^2 + … + ar^(n-1) + ar^n となります 続けます (1) - (2) を計算すると (1-r) Sn = a - ar^n = a(1 - r^n) なので、r ≠ 1 のときに Sn = a(1 - r^n) / (1 - r) です これも解説すると Sn は 1 × Sn と同じなので 敢えて 1 × Sn で書くと 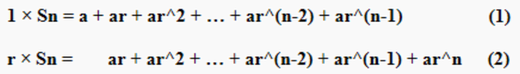 となります (2) の右辺をわざと右にずらして書いています 見てわかる通り (1) と (2) の右辺で ar+ ar^2 + … + ar^(n-1) が共通です なので、(1) - (2) を計算すると 左辺は 1 × Sn - r × Sn = (1-r) Sn となり 右辺は ar+ ar^2 + … + ar^(n-1) が消えてなくなり a - ar^n = a × 1 - a × r^n = a(1 - r^n) だけが残り (1 - r) Sn = a(1 - r^n) となります ここで、Sn = … の式にするために 両辺を 1 - r で割りたいのですが 0 で割ることはできないので (これは数学のルール) 1 - r ≠ 0 すなわち r ≠ 1 のときという条件をつけて 両辺を 1 - r で割って Sn = a(1 - r^n) / (1 - r) と計算しています 緋山: ここまではよくわかりました !(^^)! 教授: -1 < r < 1 のとき n → +∞ とすると r^n → 0 となるので Sn → a(1 - 0) / (1 - r) = a/(1 - r) に近づくこととなります これも説明すると 0 < r < 1 のときに r^n がどうなるかを考えてみましょう 重要なのは 正の数(0より大きい数)に 1 より小さい正の数をかけると元の数より必ず小さくなる ということです なので、0 < r < 1 だとすると r は 1 より小さい正の数なので r よりも r^2 = r × r の方が小さくなり r^2 よりも r^3 = r^2 × r の方が小さくなり r^3 よりも r^4 = r^3 × r の方が小さくなり… を繰り返して r^(n-1) よりも r^n = r^(n-1) × r の方が小さくなります ここで n はとんでもなく大きい自然数だと思って下さい r は正の数ですから、r^n は正の数、要するに r^n > 0 です 本当は厳密な議論が必要になりますが n = 100 → n = 1000 → n = 10000 → n = 100000 みたいに n を大きくしていくと、r^n は 0 に近づいていきます (n → +∞ とすると r^n → 0) なので、n を大きくしていくと Sn = a(1 - r^n) / (1 - r) の r^n も 0 に近づくので Sn は a(1 - 0) / (1 - r) = a / (1 - r) に近づきます 要するに、n を大きくしていくと (n → +∞) Sn は a / (1 - r) に近づきます Sn → a / (1 - r) なので a = 0.9 r = 0.1 = 1/10 とおくと Sn = 0.99999… は 0.9 / (1 - 0.1) = 0.9/0.9 = 1 に近づく ことになります ※ 0.999…9 (1より小さい数)と 0.9999… とは違います 緋山: Sn = 0.99999… というのは? 教授: n → +∞ としたときの Sn が 0.99999… ( 0.99999… = 0.9 + 0.09 + 0.009 + 0.0009 + 0.00009 + … ) になるのはいいでしょうか? (もちろん、a = 0.9 かつ r = 0.1 のとき、です) これが成り立つのは a = 0.9 ar = 0.09 ar^2 = 0.009 ar^3 = 0.0009 … となるのもいいでしょうか? 一方で、Sn → a/(1 - r) = 1 (n → +∞) だったので 0.99999… = 1 が 結論付けられます 【 0.999…9 のように9の連続を途中で止めると 1 より小さい数になりますが 0.999 … と無限に続けると 1 になります 】 緋山: ありがとうございます♪ めちゃくちゃわかりやすかったです あと原理的?な質問になりますが 0で割ったらおかしくなるとか 1との距離を 無限に小さくする=ゼロにする とかいったことから考えると 0と無限というのは 数学においては 定義して使わないといけない やっかいなものなのですか? ぶっちゃけたいい方をすると 0と無限に自然科学としての数学の限界があると言えますか? 教授: ゼロと無限の話ですか いいところを突いてきましたね 緋山さんって 正直なところ数学は本当に苦手だと思うのですが 核心がどこにあるかを感じる能力が高いですね まず最初に区別をしておきたいことは 0 は数字ですが、無限は数字ではないということす 0 は特殊な数字と言っていいかもしれませんが 0 が特殊なのは割り算を行えないことだけで それ以外は別に難しいことはないと思います 一方で、無限については 概念を明確にする必要が出てくるので 面倒な存在だと思いますよ 【 ゼロで割ってはいけない A÷B=Z の Zを求めるのは B×Z=A の Zを求めるのと一緒 というのが割り算の定義です 例えば、3÷0=Z なら 0×Z=3 の Zを求めるのと一緒 ということになりますが、そんな数はありません → 不能また不可という また、0÷0=Z なら 0×Z=0 の Zを求めるのと一緒 ということになりますが、この場合、全ての数が当てはまります → 不定という ゼロで割ると∞になる? 6÷3 = 2 この計算の意味は 3を2個集めると6になる ことを意味しています 6÷0 = Z では 0はいくつ集めても0のまま、無限大集めても0のままです 6にはなりません つまり、6÷0 = ∞ ではなく 6÷0 = は、不能・不可であって 答えがありません (0をZ個集めると6になるのZに当てはまる数がない) 但し、割る数を限りなく0に近づけたとき その答えは無限に大きくなります ということは 割る数が0になれば、無限大になるはずです これに対し、数学では 答えが出せないので 「ゼロで割ってはいけない」という法則を立てた と言えるでしょう フランスパンを限りなく小さくしていくと = 限りなくゼロに近づけていくと もとのフランスパンに戻すときの数は 限りなく大きい数( = 無限大)になります ところが、大きさが限りなくゼロに近いパンが ゼロの大きさになったとたんに 限りなく小さいパンではなくなってしまうのです ということは ゼロが、限りなく小さい数でなく 限りなくゼロに近い数が、限りなく小さい数である という理屈(パラドックス)が成り立ちます ちなみに、無限小と、負の無限大(-∞)とは、違います 無限小とは、ゼロに限りなく近い数をいいます ゼロを無限小と考える立場もあるようです 】 ヒルベルトの 「無限ホテルのパラドックス」を考察する 快足亀のパラドックス (ひとつ戻る) |
|