ヒルベルトの 「無限ホテルの パラドックス」を考察する  まえおき 物理学と数学の「正しい」の違いについて 知り合いの国立大学のアルゴリズム&人工知能の教授に 聞いたときの教授のお話です 【 物理学というのは仮説立てて、それによる帰結を導き (ここまでは数学の話) 帰結が実際に観測されるかを確かめて、確認されたら採用されます 数学的に書くと、p が仮説 q1, q2, ..., qn が帰結だとすると p ならば q1, p ならば q2 ..., p ならば qn が、全て数学的に証明されていて さらに、q1, q2, ..., qn が 全て実験的に観測された状況になれば p が正しいとして採用されます #一般に n が小さいときには、p は仮説として保留されます ぶっちゃけた言い方をすると 状況証拠を積み重ねて正しさを示します 但し、p が厳密に正しいと証明されたわけではありません 正しいと信じるに値する という言い方が正しいと思います このような証明の仕方を「帰納証明」と言いますが 自然科学における正しさは、全て帰納証明に基づいています ですから、自然科学において「絶対に正しい」という言葉は嘘です 状況証拠でしかない以上、絶対的な正しさは証明できないのです これが自然科学の限界とも言えます 昔、「原子力発電所は絶対に安全」と言っていた人は 完全に詐欺師です 帰納証明に絶対はありません 】 これに対し 【 数学というのは、自然科学(物理学、化学、天文学など) とは違い、数学自身が研究対象の学問です それゆえ証明された数式は 査読(専門家による検証)ミスがない限りは 数学上では、絶対に「正しい」のです 数学の証明は 演繹(えんえき)法の代表である 「三段論法」を繰り返えすことによりなされます 三段論法とは 前提条件 A=B B=C → 結論 A=C です 演繹法は、A=B B=C という法則(公理)から A=C という新たな法則を、導き出していくわけです 演繹法は、前提条件が正しければ 導き出される結論も必ず正しくなります これは、演繹法は 前提条件 A=B B=C を A=C に、言い換えているだけだからです 】 この「無限ホテルのパラドックス」は 数学的に「正しい」とされています ① 満室だけど宿泊可能? 本題に入ります このパラドックスは 現代数学の父と称される ヒルベルト(1862~1943・ドイツの数学者)が考案したことから 正式には「ヒルベルトの無限ホテルのパラドックス」 といいます ≪無限≫の概念を理解させるために作ったパラドックスらしいです 99%の人が理解不能なパラドックスなんだそうです いきなり文章では辛いかもなので https://www.youtube.com/watch?v=jqLQXxJc428 ダークぱんだ さんの【ゆっくり解説チャンネル】 に、とても分かりやすい説明があります このホテルは 前提① : 満室である 前提② : 客室が無限にある そこへ1人の客が「宿泊したい」とやってきます 客室が有限なふつうのホテルなら 「満室である」 = 「新たに来た客を泊めることはできない」です ところが、無限ホテルでは 客室が無限なので 1号室 → 2号室 2号室 → 3号室 3号室 → 4号室 4号室 → 5号室 というように 宿泊しているお客に1つずつズレてもらって 最初の部屋を空けることで 新たに来た客を泊めることはできる 30人の団体がきたならば 1号室 → 31号室 2号室 → 32号室 3号室 → 33号室 4号室 → 34号室 に移動してもらえばいい といった話です 満室なのに、新たな客を泊めることができる → 人の直感に反する = パラドックス ということです では、無限の数の団体が来たならどうでしょうか? 自然数は、1、2、3、4、5・・・・と、無限個あります 奇数は、1、3、5、7、9・・・・と、無限個あります 自然数と奇数はどちらが多いでしょうか? 有限なグループで考えれば もちろん自然数の方が、奇数よりも2倍多いですが 無限なグループで考えれば、数は一緒です 実数の場合、0と1の間を埋めるのに 100等分、1000等分、10000等分・・・・ とどこまでも間隔を狭めることができます これに対して、整数の場合、間を埋めることができません これが、実数の連続性であり 整数の離散性(とびひびの値を示す性格)です そして、自然数も、奇数も とびとびの間隔=濃度 が一緒なのです 濃度が一緒ということは 1つ1つの数字が「一対一対応」である ということです なので、無限なグループで考えれば 自然数も、奇数も、数は一緒なのです 自然数の持つ濃度のことを「アレフ0」といいます なお、≪無限個なら、どんな無限個も同じである≫ この従来の数学者の考えに対し 集合論を確立した カントール(1845~1918・ドイツで活躍した数学者)は 「そうではない 無限にも濃度がある」と主張しました 要するに、無限にもレベルというかランクがある といった考えです アレフは、無限集合の濃度(あるいは大きさ)を示す単位です では、実数の無限集合は、アレフ1なのでしょうか? じつは、自然数の濃度(アレフ0)と 実数の濃度の間にも、中間の濃度があるのではないか? という議論があり、確定されていないのです また、自然数の濃度のことを指して「可算濃度」といい その無限のことを「可算無限」といいます 「可算」というのは1つ、2つ、3つ・・・・という具合に 番号づけして数えられるという意味です 無限の数の団体が来たと言っても 1人、2人、3人・・・・ と数えることのできる自然数の濃度をもつ加算無限です 前述したとおり、無限で考えたとき 自然数の濃度と、奇数また偶数の濃度は一緒で 自然数と、奇数の数も一緒です なので 無限の数の団体客がきたら 全ての宿泊客に、部屋番号×2の部屋に移ってもらえばよい 1号室 → 2号室 2号室 → 4号室 3号室 → 6号室 4号室 → 8号室 ということになります こうして、奇数の数の無限個の部屋を空ければ 自然数の無限の客を泊めることができる ということです まず、【満室】とは ≪部屋の数とお客の数が一緒≫ という以外にはありません なので、最初の段階で【満室】を成立させるには お客の数も無限である という前提が成り立ちます この段階では【満室】なので 新たな宿泊客は、止めることはできません ところが【満室】から 客が1人来ようとようと、無限の数 来ようと ≪無限ホテル≫においては 無限に客室があるのだから、泊めることができる という理屈なのです これは、単に ≪無限≫という概念を主張しているだけなので 正しいも、間違えもありません しかし、ならば 最初の段階で【満室】であるという前提が おかしいです 客が、無限の数 来ようと 無限に客室があるのだから、泊めることができる というなら 最初の段階で【満室】であるという前提は成立しません つまり ① 最初の段階で【満室】であるという前提は 無限の客室は、無限の客で【満室】になる ということです 客の無限 = 客室の無限 というのが、≪無限≫についての定義です これに対し ② 客が、無限の数 来ようと 無限に客室があるのだから、泊めることができる というのは 客の無限 ≠ 客室の無限 というのが、≪無限≫についての定義です 両者において、定義が違う つまり、このパラドックスはパラドックスではなく 単にデタラメです ちなみに 無限の数の団体客がきたら 奇数の数の無限個の部屋を空ければよい というのはこういうことです ≪自然数で無限個の客室を 奇数で無限個の客室と、偶数で無限個の客室に分けました 3つの無限の「数」は一緒です≫ 有限の世界ならば 自然数は、奇数、偶数に対して、それぞれ2倍多いです 無限の世界においては 自然数の無限個を 奇数の無限個と、偶数の無限個に 半分ずつ分けたのにもかかわらず どの無限も濃度は一緒なので、数は一緒 ということです この考え = ②の考え からいくと 無限の客室は、限りなく存在するので たとえ無限の客が来ても、宿泊可能である ということになります なので決して【満室】にならないはずです ①の≪無限≫の定義からいくと 自然数の無限個の部屋は、全て埋まっているわけですから 奇数の無限個と、偶数の無限個に分けて 部屋の数が倍になったたところで、全ての部屋は埋まっているでしょ という話になりますよ(笑) つまり、≪無限≫といったって 定義によってどうにでもなる概念なので 〔 「概念」とは共通認識なので むしろ「観念」(概念より主観を含む)と言った方がよいかもです 〕 定義 (数学的に言うと「公理」?) をちゃんしてから 論ずるべきなのに ≪無限ホテルのパラドックス≫は 「定義」が曖昧というかデタラメなのです 話を戻します ②の考えからいくと 無限の客室は、限りなく存在するので たとえ無限の客が来ても、宿泊可能である ということになります しかし、【満室】なわけですから 最初から存在する部屋に (部屋を増やさずに) どうやって新しい客を入れるのですか? ということになります → 人の直感に反する = パラドックス そうなると ホントは、部屋を増やしていて それを、≪無限≫という言葉で騙して 【もともとあった部屋】に錯覚させているのではないのか? という疑問が、当然、湧いてきますよね では、なにをもって 部屋を増やす操作をしているのにもかかわらず (操作をしなければ、空き室がないので 新たな客を泊めることはできない) ≪もともと空き室が存在していた≫ と思い込ませているのでしょうか? これについては ∞ + 1 = ∞ という理屈が考えられます つまり、無限の部屋数は + 1 した ( = 1つ部屋を増やした) ところで、無限の部屋数のままで、変化しない だから、もともと存在した部屋 である ( = 部屋を増やしていない) といっためちゃくちゃな論理です めちゃくちゃといっても 【満室】だけど、無限ホテルだから【 空き室】はいくらでもある という話と大差ないですよ(笑) むしろマシなくらいです この論理からいくと ≪無限ホテル≫は、【無限に部屋があるホテル】ではなく ホントは、【部屋を増やす操作によって 後出しじゃんけんのように、限りなく (無限に) 新な部屋をつくることができるホテル】が正体ということになります それはともかく、単純に考えると このパラドックスは 有限世界においてどのような状況 (満室) にあろうと 無限は、有限とは別の原理のものである (もともと空き室がある) といった主張なのではないでしょうか? ところが、≪無限ホテル≫という無限世界において 【満室】である(有限) という間違えをしてしまった ということだと思います ② 数学的に「正しい」のは? 知り合いの国立大学のアルゴリズムの教授に ≪無限ホテルのパラドックス≫を説明してもらいました 教授: ≪無限ホテルのパラドックス≫で 説明していることはすべて正しいです 緋山: それはどうしてなのですか? 教授: ≪無限ホテルのパラドックス≫で 説明していることを数学的に書くと ・ N = 自然数の集合 (1, 2, 3, ...) ・ X = 0以上の整数の集合 (0, 1, 2, 3, ...) 0 (新たに来た客)を加えた集合です ・ Y = -29以上の整数の集合 (-29, -28, -27, ...) N に -29 ~ 0 の30個の要素(30人の客)を加えています ・Z = 整数の集合(..., -3, -2, -1, 0, 1, 2, 3, ...) とおくと N⊂X⊂Y⊂Z であるが |N|=|X|=|Y|=|Z| が成り立つことを言っています ここで、N⊂X は N が X の真部分集合 ( N ≠ X である部分集合)であることを表しています また、|N| は N の濃度(有限の集合の場合は要素の個数) を表しています N, X, Y, Z が全て有限集合である場合には このことは成立しません 要するに ≪無限ホテルのパラドックス≫は 自然数の集合、0以上の整数の集合 -30 以上の整数の集合 偶数の集合、奇数の集合は 全て濃度がアレフ・ゼロだと言っているに過ぎません アレフ・ゼロについても説明しましょう 例えば、X = { リンゴ、ミカン、ブドウ } で Y = { イヌ、ネコ、ネズミ } とおき f (リンゴ) = ネコ f (ミカン) = イヌ f (ブドウ) = ネズミ とおくと、f は一対一対応となります X から Y への一対一対応があるとき X の要素数と Y の要素数が等しいと定義します 次に、X を リンゴ、ミカン、ブドウではなく X = { 1, 2, 3 } とおいてみます 同じように、X から Y への一対一対応が存在します このとき、Y の要素数(濃度)を 3 と定義します 一般に、集合 Y に対して X = { 1, 2, ..., n } とおいたときに X から Y への一対一対応が存在するとき |Y| = n と定義します このように、n が定められるとき Y を有限集合と呼びます 一方、このような n が定められない集合 Y を 無限集合と呼びます N を(全ての)自然数の集合とします N の濃度は自然数で表現することができないので アレフ・ゼロと定義しています (アレフは無限を表す一種の記号) N から集合 Y への一対一対応が存在するとき Y の濃度もアレフ・ゼロと定義します 緋山: ① 最初の段階で【満室】であるという前提は 無限の客室は、無限の客で【満室】になる 客の無限 = 客室の無限 ② 客が、無限の数 来ようと 無限に客室があるのだから、泊めることができる 客の無限 ≠ 客室の無限 ②の考えからいくと 無限の客室は、限りなく存在するので たとえ無限の客が来ても、宿泊可能である 決して【満室】にならない ということになりませんか? 教授: まず、≪無限ホテルのパラドックス≫は 【満室であるのにお客が泊められる】というパラドックスではなく 【無限に部屋がある】ことが 「有限」の世界では成立しないので 一般の人間には違和感を生じる それがこのパラドックスの正体です 緋山さんの考えは まだ、有限のときの常識に頭が引きずられていると思います その原因は ≪無限は数ではない≫ という認識が浅いことが原因だと思います アレフ0の「無限」というのは どんな数を持ってきても、それより大きい数が存在する 有限に抑えることができない という意味での無限です (アレフ0の集合を対象とする数学を、離散数学という 簡単にいうと、整数をメインとして扱う数学のこと) そもそも無限という数はないのです 「終わりがない」ことをそう呼んでいると考えた方が近いです そこを理解して これからする私の数学的な説明を聞ければ 「なんだそんなことか」というのが分かると思います 無限にいる人に1番から番号をつけます 無限にある部屋に1番から番号をつけます i 番の人に i 番の部屋を利用してもらいます ( i = 1, 2, .. .) これが最初の状況です この時点で空いている部屋はないのです = 満室 (あるならば何番目の部屋か指摘できるはずです) あとから無限の人がバスでやって来ました 彼らも1番から番号をつけます 宿泊している i 番の人は 2i 番の部屋に入ってもらいます バスで来た i 番の人は 2i - 1 番の部屋に入ってもらいます 全員が別々の部屋に入り、全ての部屋に人がいるので満室です 無限は数では無いので、a + a = a みたいな変なことが起こります ( aは自然数の濃度を表していると思って下さい ) 有限である10番の部屋だけで見てみると 最初は10番の人が入っていたのに 入れ替えたときには 5番の人が入っているので 5人を追い出した形になっているのですが (番号的に) 後ろにいくらでも部屋があるので 吸収できるという訳です 緋山: なるほど・・・ そんな発想があったとは・・・・ これは、恐れ入り谷の鬼子母神 (恐れ入りました) です ≪無限ホテル≫とは 1人の客のときも満室、30人の客のときも満室 無限の客のときも満室 つねに満室の状況にある イメージでいうと 【際限なく伸びることのできるホテル】ということですね!! 一般に正解かと思われている ② 無限の客室は、限りなく存在するので たとえ無限の客が来ても、宿泊可能である = 満室にならない よりも むしろ ① 最初の段階で【満室】であるという前提は 無限の客室は、無限の客で【満室】になる → つねに満室になる が正解だったのですね 教授: 無限の世界は 数に終わりがないことを悪用して 我々の直感に反するコト、常識に反するコトを成立させているだけ と言えるのかもしれません なので、私は無限の世界を扱うことを避けています 笑 緋山: 別次元のコトで、≪人間の直感に反する≫とか ≪人間の常識に反する≫とか 聞くと 【天才だけが理解できる】みたいな 言葉のもつバーチャルな世界に 引きずり込まれてしまいます(笑) 数学や物理学がこういうので商売しちゃダメですよね 宗教じゃないのだから・・・・ どんなにすごい話かと思ったら 一休さんのとんち話「この橋渡るべからず」 なんかとそんなに変わりません ちなみに、とんち話も、常識に反するコトを言うことだけど(笑) 陽天さんは ≪無限大? そんなものは数学屋が勝手に考えた概念やで≫ ≪無限大と0は、数学において大きな問題や つまり、ここらが自然科学としての数学の限界と言える≫ ≪しかし、わしら工学屋だけはごまかされん ごまかしたら、モノが動かんし、モノが壊れる≫ ≪数学屋は数にしか興味がない それはそれでええ。数学は数を扱う学問やからな しかし現代物理学ちゅうんは そうした現代数学を悪用してできとることを みなに早よ知らせんとあかんな≫ と言っています 教授も【 「実際にあるのか?」という質問は 数学では愚問で、モデルとして成立する(矛盾しない) ならば存在すると考えるのが数学です 数学はあくまで数学の中という 閉じた世界で、理論を組み立てているので 物理とか、他のところで使えるかはどうでもいい話なのです 】 と述べています また、ヒルベルト自身 【 数学は決められたルール (公理と推論法則)に従って行われるゲームであり ルールを取り替えることによってできる異なるゲームは それぞれ同等である 】 と言っています (ウィキペディア「形式主義」) つまり、大学から勉強する数学は あるルールのもとになされるゲームにすぎす ゲームに真理も虚偽もないのと一緒で 現代数学の数式が、現実世界の真理を表わしている わけではないということです 現代数学の父がそう言っているのです!! 教授: ∞ + 1 = ∞ この式も厳密ではないのです 重要な点なので繰り返しますが 【∞は数ではない】からです この式を認めるためには ∞という数を定義する必要があります でも、そんな定義はありません 緋山: 増やす・減らす という概念が すでに、無限という概念に、反するのかもしれませんね なぜなら、無限から、プラスするマイナスする というのは、≪無限から≫を ≪無限の数から≫ (= ある数から) というように 有限化してしまっているからです ③ 無限の乱用 緋山: 以前、フラクタルについて教授に聞いたとき 「無限」について触れましたね フラクタルとは 図形全体(自分)の中に 相似な形(自分と同じ小さな形)を含む図形です 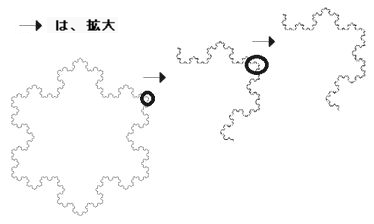 左の図形は、コッホ雪片と呼ばれています コッホ曲線というフラクタルによってできています フラクタルの中でもとくに有名なもの1つに 「コッホ曲線」があります コッホ曲線は、スウェーデンの数学者 ヘルゲ・フォン・コッホ(1870~1924)が考案したフラクタルです 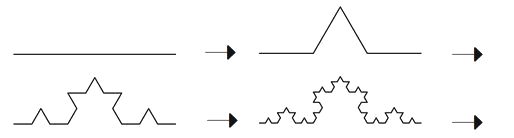 線を三等分し、その真ん中の線を1辺とする 正三角形を作っていくことを繰り返します この操作を無限に繰り返すとコッホ曲線になるとされます 無限に繰り返すと、もはや直線でできた図形としては複雑すぎる ということで曲線というそうです 自然界における コッホ曲線の近似として「海岸線」があげられています フラクタルの発見は、イギリスの気象学者 ルイス・フライ・リチャードソン(1881~1953)だといいます 彼は、国境を接するスペインとポルトガルが 国境線について、それぞれ別の値を主張していたことから 国境線の長さは、用いる地図の縮尺によって 変化することを発見したといいます これが、リチャードソンの示した 「海岸線のパラドックス」です 海岸線のパラドックスとは 海岸線の長さが、フラクタル的性質をもつため 1つに確定しないというものです
海岸線を測るとき、定規の長きが長いと 入り組んだ場所は測れません 正確に測るためには、短い定規を使う必要がありますが 短い定規でより正確に測ると、その分、海岸線の長さが長くなります 正確に測れば、測るほど、海岸線は長くなります 教授は、コッホ曲線の ≪操作を無限回数 繰り返すとコッホ曲線になる≫ ということについて、以下のように言っていましたね 【 教授: コッホ曲線の各線分___を _∧_ に置き換える操作を 無限回数行うと言いいますが、そもそも無限という数はないのです 「終わりがない」ことをそう呼んでいると考えた方が近いです ですので、置き換え操作を無限回数行うと 長さが無限になると言っていますが 正しくは ≪置き換え操作をくり返し続ければ 長さも長くなり続ける≫というのが正しいです 海岸線が、コッホ曲線だとすると 与えられた長さまで測ると 後出しじゃんけんのように、新な長さが次々に つくられていくという話になりますが 海岸線は別に自力でコッホ曲線の置き換え操作を 行っているわけではないので どこかで、後出しじゃんけんができなくなります くり返しに限りが来ます 無限にはなりえないのです 要するに、海岸線は操作回数が固定されたコッホ曲線です 長さを測定する側が コッホ曲線に合わせた小さな定規を持ち込むことで 長さが確定してしまうはずです 緋山: 「無限にギザギザしている図形(フラクタル)は 自己相似なので どんなに細かく分解して無限に ギザギザしている」 という話を 有名な数学・物理の教育系ユーチューバーのヨビノリさんが 動画でしていますが これについてはどうですか? 教授: 実際に無限にギザギザしている図形なんて存在しませんよ まあ、仮に電子や陽子とか もっと細かい物理の最小単位のレベルで フラクタルになっていると仮定してもいいですけど 結局そこで終わりって話です フラクタルの長さについては 「操作を無限回 行う」というところに 怪しさが隠されていると思えます 無限の乱用があるように思えます 】 緋山: そこで、あらためてお聞きします 【 海岸線は別に自力でコッホ曲線の置き換え操作を 行っているわけではないので どこかで、後出しじゃんけんができなくなります くり返しに限りが来ます 無限にはなりえないのです 】というのは 置き換え操作を行っている人間が有限の存在だから という意味ですか? 教授: わたしが、置き換えを無限に行えないと言ったのは 物理的な限界のためです 海岸線は、(一部の)人間が、勝手に フラクタル(コッホ曲線)だ と言っているだけですが コッホ曲線も同じです 置き換え規則を繰り返すと 線分が、限りなく小さく(短く)なります こんな風に考えてみて下さい 野球ボールを並べて 1cm単位の折れ線を作ることができますか? もちろん答えは NO ですよね 置き換え操作を繰り返すと 線分の長さが 1cmどころか 1mm, 1μm, ... といくらでも小さくなっていきます それを野球ボールで構成することは不可能です 野球ボールを原子に置き換えても一緒です ならば、表せる線分の長さにどこかで限界がやってくるのです 価値論 【 数学・物理学 編 】 フラクタルの理論について ① ② おまけ 海岸線のパラドックス 海岸線のパラドックスについておさらいします 【 ある島の海岸線を、長さ1kmの定規で測ったところ 定規が5本分の長さでした なので、海岸線の長さは 1km×5=5km です ただ、定規が長かったので 海岸が入り組んでいる場所は測れませんでした もう少し正確に測るために、0.5km の定規を使ってみました すると、海岸線の長さは定規16本分 0.5km×16=8km となりました 1kmの定規で測ったときより、海岸線が3km 長くなりました さらに定規の長さを短くして測ると、海岸線はさらに長くなりました 地図を拡大していくと、見えていなかった細かいデコボコが見えてきます それをもっと短い定規で、正確に測ると、さらに海岸線は長くなりました いくらでも拡大していくことができるので 海岸線は、果てしなく伸びていき、長さは、無限大になってしまう 】 教授の解答を記します 単なるパラドックスの話なので 真面目に考えない方がいいですよ と言いたいところですが、笑 スッキリしないと思うので 何がおかしいのかをお話ししておきます 海岸線を長い定規で測るとします 定規は直線ですが、海岸線は曲線です ですので、曲線を無視して定規で測ると 実際の距離より短くなります では、定規の長さを短くします 先ほどよりは小回りが利くので 測定結果は実際の曲線に長さに近づき 長くなります さらに定規の長さを短くします さらに小回りが利くので さらに測定結果は先ほどより長くなります 海岸線はどこまで細かく見ても曲線なので 定規の長さを短くし続ければ 測定結果は長くなり続ける 測定結果が長くなり続けるということは 海岸線の長さは無限ではないか? と言うのが「海岸線のパラドックス」の主張です このパラドックスは 測れないから無限大と言っているわけではなくて 定規の長さを短くすれば測定結果が長くなるから 定規の長さを(0にならないようにして) 永遠に短くし続ければ 測定結果も永遠に長くなり続ける=長さは無限である という主張です このパラドックスの誤りは 測定結果も永遠に長くなり続ける=長さは無限である にあります # そもそも、定規の長さを永遠に短くし続けなければならない 海岸が存在するのかという話もありますが 笑 先ほどの例ですが 最初は5km、次は3km 長くなっわけですが 定規を短くするのが n 回目のときに 長さが前回測定結果より 5× 0.6^n だけ増えるとします 0.6^n とは 0.6 の n 乗 すなわち、0.6 を n 回かけた数です 要するに、最初は 5km で 次に 5×0.6=3km 長くなって その次は 3×0.6=1.8km 長くなって さらに 1.8×0.6=1.08km 長くなり 1.08×0.6=0.648km 長くなり… と永遠に繰り返したとします これを繰り返すと 確かに永遠に測定結果は長くなり続けるのですが 無限に続けても 5÷(1-0.6)=12.5km にしかならないことが 計算できます 要するに 5×(1+0.6+0.6^2+0.6^3+ …)=12.5 となります つまり、無限に足し続けたからといって 足した結果が無限になるとは限らないのです それが今回のパラドックスの正体です # アキレスと亀のパラドックス と本質的に変わらないのです 【 5÷(1-0.6)=12.5km について 最初の長さが 5km 次に、長さが 5×0.6km=3km 増える 次に、5+3=8km から 長さが 5×0.6^2=1.8km 増える 次に、8+1.8=9.8km から 長さが 5×0.6^3=1.08km 増える・・・・ とします 5km から (n-1)回まで長さが増えたときの合計の長さをLnとします Ln=5+(5×0.6)+(5×0.6^2 )+ … +(5×0.6^{n-1}) これは、初項 a=5、 公比 r=0.6 の等比数列の和になっています この式の和は簡単に求められ、公式にもなっていますが ちゃんと求め方を書いておきます Lnを 0.6倍すると 0.6×Ln=(5×0.6)+(5×0.6^2)+ … + (5×0.6^{n-1})+(5×0.6^n) となります 0.6^n とは 0.6 の n 乗 すなわち、0.6 を n 回かけた数です 5を0.6倍すると、(5×0.6) (5×0.6)を0.6倍すると、(5×0.6^2) (5×0.6^{n-1})を0.6倍すると、(5×0.6^n) となります Lnから 0.6×Lnを引くと Ln= 5+(5×0.6)+(5×0.6^2)+ … +(5×0.6^{n-1}) 0.6×Ln=(5×0.6)+(5×0.6^2)+ … +(5×0.6^{n-1})+(5×0.6^n) 共通の部分がなくなって Ln-(0.6×Ln)は、5-(5×0.6^n) となります つまり、Ln-(0.6×Ln)=5-(5×0.6^n) です 左辺をLn でくくると (1-0.6)×Ln になります 右辺を5 でくくると 5×(1-0.6^n) になるので (1-0.6)×Ln=5×(1-0.6^n) さらに、Ln=5×(1-0.6^n)÷(1-0.6) となります これでn を大きくしていくと 0.6^n は、0に近づきます 0.6×0.6=0.36 0.36×0.6=0.216 0.216×0.6= ・・・・ これを繰り返すと 0 に近づくのがわかると思います n が無限のとき、0.6^n=0 なので n が無限ならば Ln=5×(1-0.6^n)÷(1-0.6) は Ln=5×(1-0)÷(1-0.6) Ln=5×(1)÷×(0.4)=25/2=12.5 になるわけです 】 スミスさんの子供(2人の子供の性別問題) 1/3×3 = 1 のはずなのに 0.3333…×3 = 0.9999… のパラドックス (ひとつ戻る) |
|