スミスさんの子供 (2人の子供の性別問題) 火曜日生まれの女の子   「スミスさんの子供」は 海外では「Boy or Girl paradox」 (少年か少女かのパラドックス・2人の子供の性別問題)と呼ばれ 古くから大論争を巻き起こしてきた確率の問題です 確率の世界では モンティホール問題と双璧をなすパラドックスとして知られています アリストテレスさんの動画 【パラドックス】2人の子供問題 ~めちゃくちゃ確率の理解が深まります~ https://www.youtube.com/watch?v=8pyoUbZ-ij4 を参考にさせていただきました 問題 ① スミスさんには、2人の子供がいます 第一子は女の子です 2人が姉妹である確率を求めよ 但し、男女の生まれる確率は50%とする (以下の問題も同様)  第一子の扉が開かれていて 女の子であることが確定しています 結局、問題①は、第二子の扉に 男の子がいるか、女の子がいるかの確率を聞いているので 答えは1/2になります 問題 ② スミスさんには、2人の子供がいます 少なくとも1人は女の子です 2人が姉妹である確率を求めよ この問題では  どちらか1つの扉、また2つの扉に 女の子がいることが前提条件となっています  2人の子供のパターンは、4つありますが 女の子がいることが前提条件となっているので、男・男は消えます 前提条件を満たすパータンは3つです 問題②は、前提条件を満たす3つのうち 「2人が姉妹(女・女)である確率を求めよ」なので 答えは1/3になります 以上のように ①と②で違った結果になるのが 人間の直感に反する → パラドックスになっている というわけです 問題 ③ (超難問) スミスさんには、2人の子供がいます 2人が姉妹である確率を求めよ ※ あなたはスミスさんの子供の1人が出かけていくのを見ました 答えを先に明かすと1/2になります なぜ ( ̄▽ ̄;)? となりますよね  知り合いの国立大学の アルゴリズムの教授に聞いてみました 教授: 扉1と扉2のそれぞれに子どもが1人ずつ隠れている どちらの扉も、男の子と女の子が半々の確率で入っているとします 司会者は中に男の子が入っているか 女の子が入っているかを知っているとします 問題②は、司会者が女の子が入っている扉を開けて 「もう片方の扉には男の子と女の子のどちらが入っているでしょう?」 と聞いている状況になります 問題③は、司会者がルーレットか何かで開ける扉を決定し その決定に従って扉を開けたら女の子がいた状態で 「残りの扉には男の子と女の子のどちらが入っているでしょう?」 と聞いている状況になります 要するに、問題②は 最初に開ける扉が作為的であるのに対して 問題③は、完全にランダムに決定していることになります この違いが確率の違いに大きく作用しています  問題②では、確率的な要素は扉1と扉2に 男の子がいるか女の子がいるかだけです 問題③では、それに加えてどちらの扉を開けたかになります 問題②の組合せは 扉1の子の性別、扉2の子の性別で 女、女 ○ 女、男 ○ 男、女 ○ 男、男 × が均等に起こるのですが このうち、最後の「男、男」だけが除外され 残り3つが均等に起こりうるので 「女、女」である確率は1/3となります 一方、問題③は 扉1の子の性別、扉2の子の性別、開けた扉 の組合せで 女、女、1 ○ 女、女、2 ○ 女、男、1 ○ 女、男、2 × 男、女、1 × 男、女、2 ○ 男、男、1 × 男、男、2 × が均等に起こり このうち×がついているものが除外され 残りが均等に起こりうるので 「女、女、1」+「女、女、2」が起こる確率は 2/4 = 1/2 となります 緋山: 「スミスさんの子供」をネットで調べていくと 問題②のケースを 【 スミスさんには、2人の子供がいます スミスさんの家では 五月の節句には、鯉のぼりを掲げます (1人は男の子です) 2人が兄弟である確率を求めよ 】  問題③ケースを 【 スミスさんには、2人の子供がいます 2人が兄弟である確率を求めよ ※ あなたがスミスさんの家に電話をすると男の子が出ました 】 としているサイトがありました 面白いですね 正己の異論・反論 https://self.blog.ss-blog.jp/2008-08-05  問題 ④ 応用問題 (火曜日生まれの女の子) スミスさんには、2人の子供がいます 少なくとも1人は火曜日に生まれた女の子です 2人が姉妹である確率を求めよ 問題②の応用問題です 教授: 応用問題は 扉1の子の性別、扉2の子の性別 扉1の子の生まれた曜日、扉2の子の生まれた曜日 の4つ組を考えています そうすると 前提条件(火曜日生まれの女の子がいる)に該当する (女、女、日、火) (女、女、月、火) (女、女、火、日) (女、女、火、月) (女、女、火、火) (女、女、火、水) (女、女、火、木) (女、女、火、金) (女、女、火、土) (女、女、水、火) (女、女、木、火) (女、女、金、火) (女、女、土、火) (女、男、火、日) (女、男、火、月) (女、男、火、火) (女、男、火、水) (女、男、火、木) (女、男、火、金) (女、男、火、土) (男、女、日、火) (男、女、月、火) (男、女、火、火) (男、女、水、火) (男、女、木、火) (男、女、金、火) (男、女、土、火) 27通り中、女、女であるのは13通りとなるので 13/27 という確率になります 緋山: 2 (扉1の子の性別) × 2 (扉2の子の性別) × 7 (もう一人が生まれた曜日) = 28通り のように思えますが 扉1 姉・火 扉2 妹・火 扉2 妹・火 扉1 姉・火 が重複するので 27通りになるわけですね 以下の図は 明日は未来だ https://sist8.com/kg というサイトより転写させていたたきました 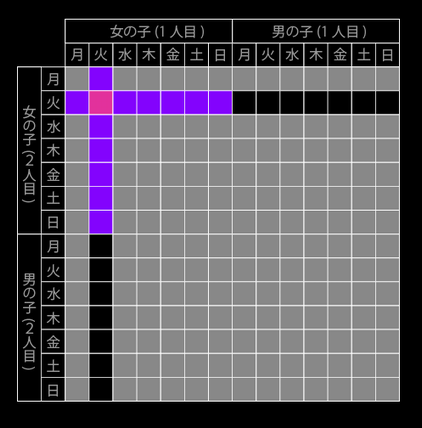 さて、ここで疑問が起きます ふつう 条件が多くなる → 起こる確率が減る なのに ≪火曜日生まれ≫という条件が加わると 1/3(33.3%) → 13/27(48.1%) になるってどういうこと? と思いますよね これについても 明日は未来だ というサイト に、詳しいい解説があります 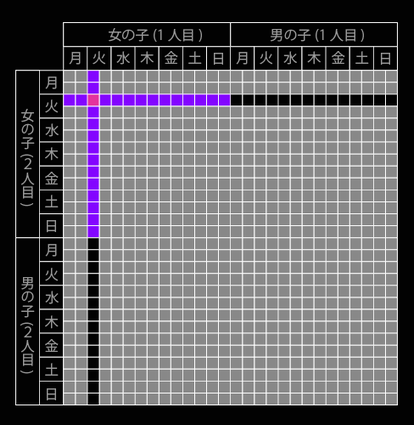 なんと、≪火曜日生まれ≫に さらに≪午前中≫という厳しい条件を付けて 【 火曜日の午前中生まれの女の子がいます 】にすると 確率はさらに上がり 2人が姉妹である確率は 27/55(49.0%)になる とあります 厳しい条件が付くほど、確率は50%(1/2)に近づくそうです 問題②の 「少なくとも1人は女の子です」だと その子が第一子なのか第二子なのか特定されていません (姉妹である確率1/3) これに対して 問題①の 「第一子は女の子です」だと その子が第一子であると特定されています (姉妹である確率1/2) 応用問題は②と①の中間にあり 女の子が特定されるほど = 重複が少なくなるほど ①(確率1/2)へと近づくそうです 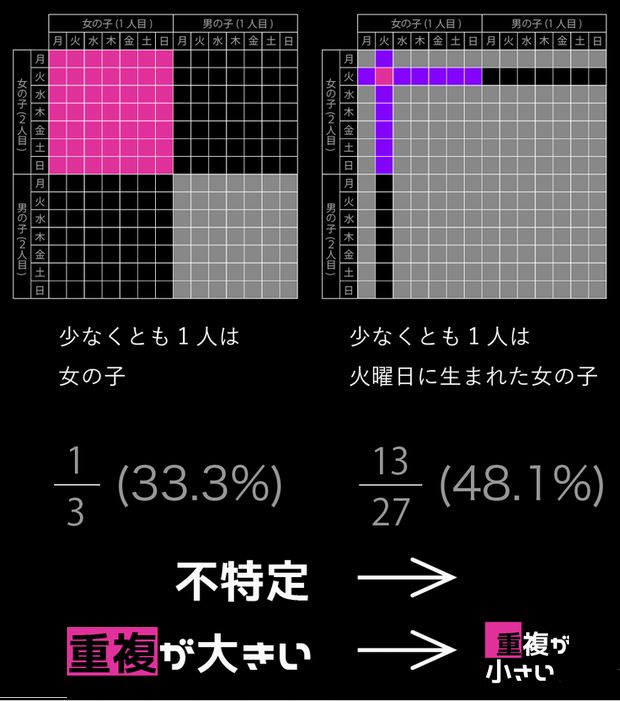 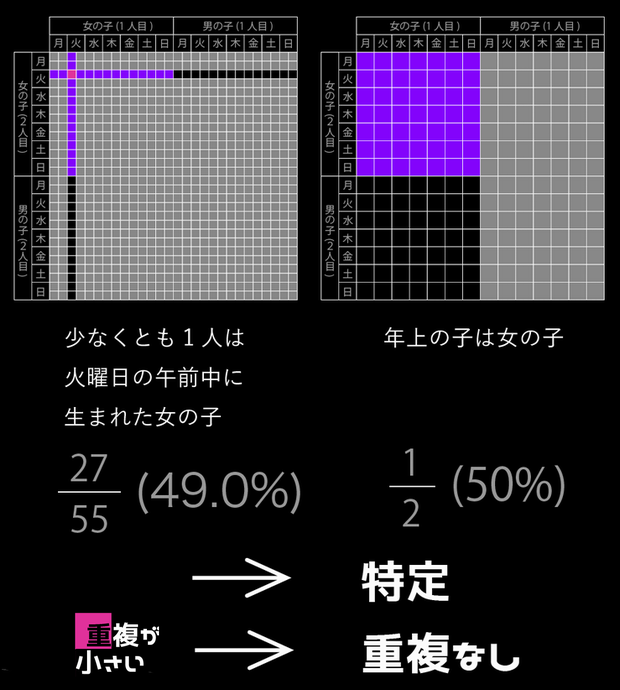 問題が 【 スミスさんには、2人の子供がいます 1人はキャロラインという名前の女の子です 2人が姉妹である確率を求めよ 】だと 姉妹に同じ名前を付けることはないので → 重複がない = 確率が1/2になる そうです 整理すると 正解が起こる確率 = 正解が起こる数 / 前提条件を満たす数 なので → 姉妹となる場合の数 ÷ 少なくとも1人は火曜日生まれの女の子がいる場合の数 → 姉妹となる場合の数 ÷ 姉妹となる場合の数+姉妹とならない場合の数 → 紫のマス / (紫のマス + 黒のマス) となります 結局、条件を厳しくすればすほど なぜ確率は上昇するのか? 条件をしぼることで 「姉妹となる」(紫のマス)の割合が増えるというよりも 「姉妹にならない」(黒のマス)の割合が下がるため 相対的に「姉妹となる」確率が上昇するらしいです それでも もう一つよくわからないので 教授に聞いてみましょう!! 緋山: ふつう 条件が多くなる → 起こる確率が減る なのに 曜日という条件が加わると 1/3(33.3%) → 13/27(48.1%) になるってどういうことですか? 教授: それは考えている母集団が違うからです 問題②の前提条件が起こる確率は 3/4 = 0.75 です (4通りのうち〇が3通り) 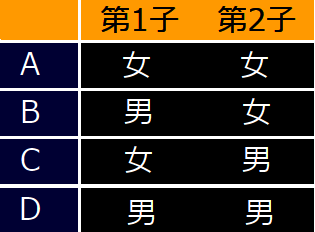 応用問題の方は、全ての場合をリストしませんでしたが 前提条件が起こりうる確率は 2×2×7×7=196通りのうちの27通りで、27 /196 = 0.137… です  要するに、応用問題の方は レアケースの中での確率を言っているだけです ヒルベルトの 「無限ホテルのパラドックス」を考察する (ひとつ戻る) |
|