EMANの物理学のHさん 顔洗って出直してくれ!!③
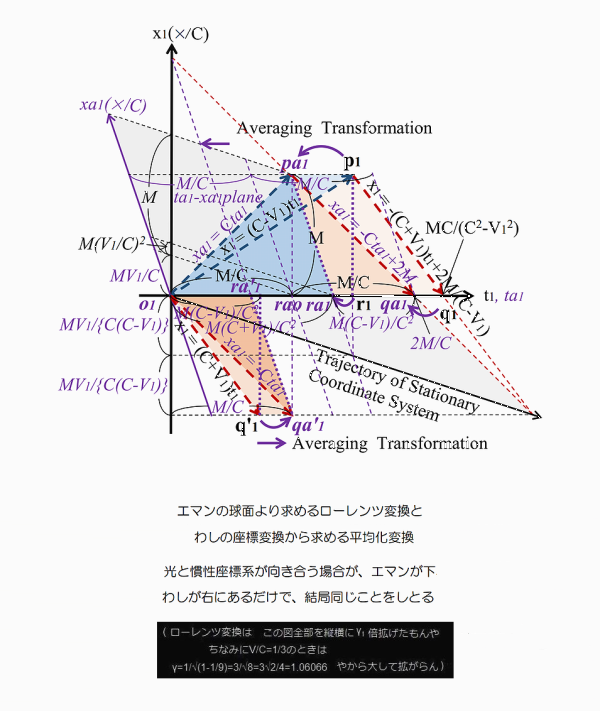
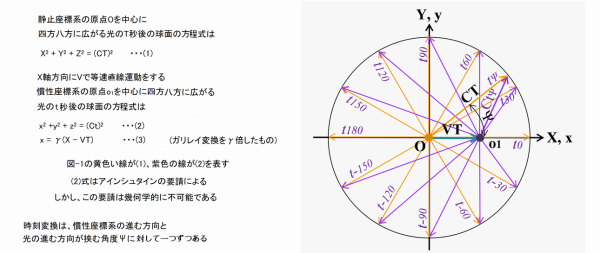
Cは光速、Vは電車(慣性系)の速度 (図は、慣性座標系の速度Vは、光速Cの1/3となっている) Tは時間 (tばガリレイ変換後・taは平均化変換後) Xは距離 (xばガリレイ変換後・xaは平均化変換後) ローレンツ変換は Bさんの見る世界なので「距離」はBからの距離です γ(ガンマ)は、ローレンツが発明したローレンツ係数で γ = 1/√{1-(V/C)^2} なお光速は、300,000,000m/s なので 横軸の T=1秒のとき、光は X=300,000,000m のところにいます TとX が同じスケールでははみ出てしまいます そこで、X軸の値を300,000,000で割ります (X/C) そうしてやると 横軸 T=1秒のとき、縦軸 X=1 になり T=1のとき、X=1 なので 光速が、300,000,000m/s ならば、傾きが45度の直線になります 陽天: エマンはこういう図をよう描かんから ローレンツ変換の致命的な間違いに気が付かんようやな わしのは、鏡で光が反射する想定なので 戻る光(赤の点線)は、行き光(青の点線)の右にある エマンのは、行き光(青の点線)に対して 戻る光(赤の点線)は、ひっくり返って下にある 上の薄いピンク色の三角形と、下の濃いピンク色の三角形 △pa1qa1ra1と、△o1qa'1ra'1 この2つの三角形は合同や エマンは平均化変換を経由せずに 直接ローレンツ変換に行く (逆変換が同じという求め方)が 結局、同じことをしとる 慣性座標系からみた光は±Cにはならん 行きは、C^2/(C+V1) 戻りは、C^2/(C-V1) となる ローレンツ変換とは X軸のプラスとマイナスに行く光を 数字上光速にしようと試みただけや しかも失敗に終わっとる これについては論文に詳しく書いた 緋山: 球面方程式の図について どういうシチュエーションになっているのかを 教えていただけますか? 陽天: わしのは、じいさんのオリジナルと一緒です 鏡に反射した光が戻る想定にしとる それに対してエマンのは球面の想定や 実は球面やなく、X軸をプラス向きに行く光と マイナス向きに行く光を平均化しとる エマンのには鏡はないが xa1=M (Bから鏡までの距離)の点に 鏡があるわし(じいさん)の想定と同じや 緋山: ここで前提を確認しておきます プラットホームに立つAから発射された光を 数秒後にAとBが観察したとき Aから観測される同心球状に広がっていく光が そのまま電車に乗るBさんにも 同心球状の光として観測されるということを前提としています 緋山: あたかもプラットホームのAから発射された 球状(球面)の光が届くような話に思えますが 陽天: X軸方向にVで等速直線運動する慣性系Bがおる 式で表すと、 X = VT 〔 この式は、Aからみた電車およびBの位置を示している Aからみた電車およびBの位置は、VTで遠ざかっていく 〕 まず、静止系Aの座標をガリレイ変換する つまり、 x = X - VT する 〔 この式は、BからみたプラットホームおよびAの位置を示している プラットホームの位置を原点とする、つまり距離ゼロとするので x = 0 - VT → x = - VT BからみたプラットホームおよびAの位置は、- VTで遠ざかっていく 〕 ガリレイ変換したとたん 球面やなく、X軸だけの話になるんやね X = x - VT Y = y = 0 Z = z =0 つまり X 軸方向に進む光だけに限定される ということです 緋山: 球面の式は、デタラメで 幾何学的に正しいのは、X軸をプラス方向に行く光だけである そこはおいておきます 球面の式というのはB(原点o1)においても 光が同心球状(四方八方)に広がっていく という話なのですが ガリレイ変換すると、X軸に限定されてしまう なので 原点o1(Bさん)からX軸のブラス方向を行く光と X軸のマイナス方向を行く光になるわけですね!! 陽天: そうや だから、原点o1を通るxa1=Cta1と xa1=-Cta1になっとるんや 以下、緋山が解説します 原点01(電車とともに進むB)にとっては X軸をプラス方向(電車の進む方向)に行く光 マイナス方向に行く光 (どちらも行く光) これ(球面方程式)を図として描いたのがこの部分です 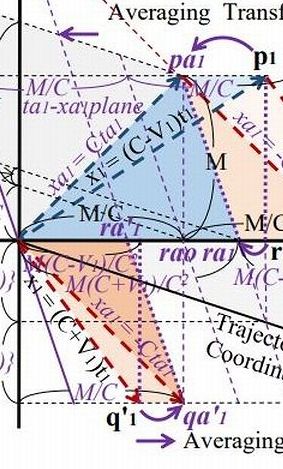 電車と同じ方向に進む光を プラス方向に行く光(青の点線)として 上に描いています 電車と向き合う方向に進む光を マイナス方向に行く光(赤の点線)として 下に描いています 次に、陽天さん(アインシュタインのオリジナル)の図を説明します 図のこの部分です 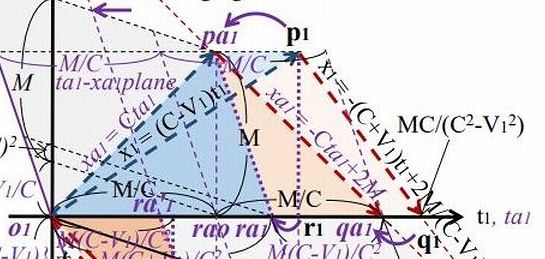 もともといたBの位置(O1)から 鏡(三角形の頂点P1)までを、行く光 (青の点線) 鏡(P1)から 電車を移動するBの位置(q1)までを、戻る光 (赤の点線) として描いています ローレンツ変換前 (Aの見る世界を、ガリレイ変換した後)の 光の進路が、不等辺三角形(O1P1q1)です 行く光(青)の相対速度は、電車の速度がマイナスされる のでBから鏡まで行くまでの時間が長い 戻る光(赤)の相対速度は、電車の速度がプラスされる ので鏡からBに戻るまでの時間が長い 車両の左端に立つBと 右端にある鏡の間の距離(М)は、つねに一緒です なので、光速不変ではないのです ローレンツ変換の肝は、この不等辺三角形を 直角二等辺三角形=光速度不変 にする 「平均化変換」です 陽天さん(アインシュタイン)の「戻る光」と 球面方程式の「マイナス方向の行く光」とは同じです 陽天さん(アインシュタイン)は 平均化変換によって o1pa1qa1の直角二等辺三角形をつくり 球面方程式では o1pa1qa´1の直角二等辺三角形をつくっているわけです 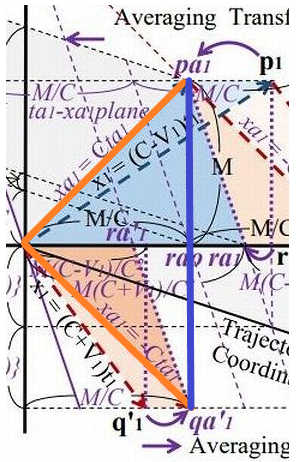 ここまでは、X軸の行く光と戻る光を平均化する変換で あとはおまけとして、「ローレンツ収縮」を取り込んだ分の変換をします X軸(水平の光)とY軸(垂直の光)の到着を一緒にするために γ(ローレンツ係数)を掛け算するのです これでローレンツ変換は、完成形となります しかし、線形変換(平均化変換)したX空間に 線形変換(平均化変換)していないY空間を縫い合わせ ローレンツ変換を完成させて 全方向からの光速不変を主張したところで 物理の大原則たる「空間の等方性」はめちゅくちゃ そんなの実空間であるわけがありません また、Y空間もちゃんと線形変換をしたならば 水平の光と垂直の光は、Bのもとに同時に到着しない = 光速不変にならない ということです 世の中には相対性理論が 完全に正しいと勘違いしとるやからがいて 仲間を増やそうと大々的に 宣伝を行っとるんをよお見かける GPSやら、ミューオンや!! こういうやからによって 間違っていることが明々白々である 相対論の布教に 人生を棒に振る信者が増えるのが えらい心配である 人に教えたり、本を出すくらい信者は わしの「ローレンツ変換は間違い」 という指摘に対して 間違いでないことを示さなあかん しかし、それは非常に難しいことやし 100%無駄な努力に終わる わしの論文に書いてあることに 反論しようとする者はおらんと思うが もしおれば、人生を捨てる覚悟でやってくれ!! 理論は信じる信じんやない (価値判断 = 必要か不必要か とか 好きか嫌いか とか の対象ではない) 正しいか間違いかや! (真偽判断のためのものである) 陽天: それから、特殊相対性理論の時間説 「速く動くと時間が遅くなる」やが ローレンツ変換から来とる 光の速度を強引に同じ値にするために 行く光のときは時間の刻みを遅くする (= 光速に電車の速度分を引く) 戻る光のときは速くする必要がある (= 光速に電車の速度分を足す) 非平均化や しかし、それでは時間が2つできてしまい 光が鏡に反射した瞬間に切り替えなあかん これでは皆を騙されん それでこの2つの時間を平均化したんが平均化変換で それをγ倍したんがローレンツ変換やったね そこで時間を平均化するとき 慣性系(電車やロケット)の速度が速いほど 時間の刻みを遅くせなあかん だから、速く進む物体の方が 時間の刻みは遅くなる ただそれだけのことや 物理現象ではない。単なる算数や EMANの物理学のHさん 顔洗って出直してくれ!!④ アインシュタインの論文の ローレンツ変換導出法 EMANの物理学のHさん 顔洗って出直してくれ!!② (ひとつ戻る) |
|