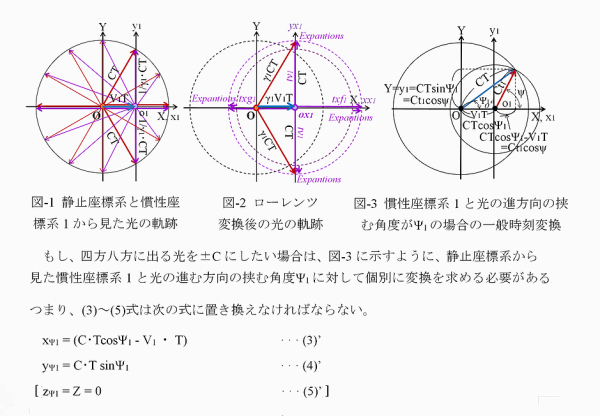
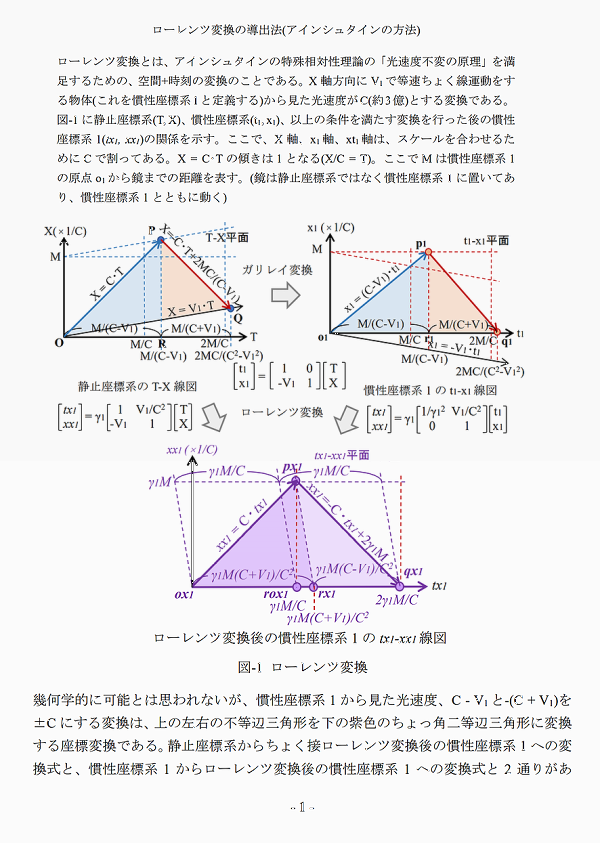
EMANの物理学のHさん 顔洗って出直してくれ!!④ アインシュタインの論文の ローレンツ変換導出法 緋山: いよいよアインシュタインが 鏡の距離を限りなく0にした理由ですね!! 陽天: ポンチ絵(スケッチ図)と解説を作って送ったる ただ、ポンチ絵も難しいで 偏微分が出てくる アインシュタインの論文のローレンツ変換の導出法や 書きなぐっただけの手書きのメモやが これ自身、論文になるぐらい高度や 一般にはわからんやろ 緋山: まず、ローレンツ変換の基本的なことから聞きます ローレンツ変換は Y空間(垂直方向の光の進路)の変換はやらないのですよね!! 陽天: ローレンツ変換は tx1 = γ1・ta1 = γ1{1/γ1^2・t1-(V1/C^2)・x1} = γ1{T-(V1/C^2)・X} xx1 = γ1・xa1 = γ1・x1 = γ1(X-V1・T) yx1 = ya1 = y1 = Y だから、Y軸は何もせん 【 なお、ローレンツ変換(tx,xx)の tx(ローレンツ変換した時刻)、xx(ローレンツ変換した距離) の式をやが 通して書くとわかりにくいので 静止系(T,X)、ガリレイ変換(t,x)、平均化変換(ta,xa) との関係から分けて書く tx1 = γ1・ta1 ta1 = 1/γ1^2・t1-(V1/C^2)・x1 t1 = T と xx1 = γ1・xa1 xa1=x1 x1 = X-V1・T となる 】 緋山: yx1 = ya1 = y1 = Y は yx1(ローレンツ変換したY空間) = ya1(平均化変換したY空間) = y1(ガリレイ変換したY空間) = Y(静止系の観測するY空間) ですね 陽天: わしはこれをおかしいと言うとる X軸方向の光を考えるときは、Y=0 Y軸方向の光を考えるときは、X=0 や だから、yx1 = ya1 = y1 = Y は間違い xx1 = γ1・xa1 xa1 = x1 と一緒なので yx1 = γ1・ya1 ya1 = y1 が正しい でないと空間の等方性がデタラメとなり、空間がゆがむ 但し、垂直方向には慣性座標系は動いてないので x1 = X-V1・T とは違い y1 = Y や 緋山: 電車は x 方向(➝) に Vの速度で進んでいるとします ある適当な位置に、物体Mがあるとします プラットホームで静止しているAさんが観測する物体Mを 電車に乗っているBさんが観測した場合 どのような関係が成り立つでしょうか? 下の図では、物体Mを電車に置かれた鏡としています Aさんが観測する鏡の位置は x,y,z,t で示され Bさんが観測する鏡の位置は、x',y',z',t' で示されます 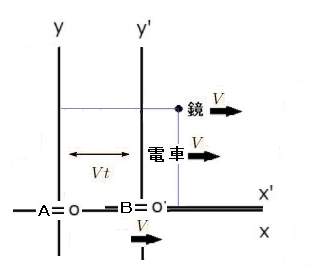 両者の関係は x' = x - vt t' = t y' = y z' = z となる これがガリレイ変換です ガリレイ変換とは、結局なにかというと 電車に乗っている次郎君が見ている 物体Mの位置(縦・横・高さ・時間)を 静止している太郎君の 座標(縦・横・高さ・時間の各軸)を基準として 表現してあげるということであり これはローレンツ変換も一緒です X軸方向の光を考えるときは、Y=0 Y軸方向の光を考えるときは、X=0 ということですが 前に Xという線空間だけの変換 において、以下のとおりに書いています 【 下の図は、三次元空間を表わしたものです 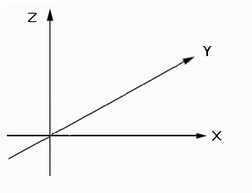 この図でいうと、水平の鏡の方向はX空間 垂直(直角)の鏡の方向はY空間となります X空間だけいじくって (=ローレンツ変換をして) X空間とY空間の 光の行って来いする時間を一緒にしたところで (光速度不変にしたところで) 物理の大原則たるべき空間の等方性は保たれていませんよね Bさんの観測する 三次元世界を線形変換するというなら X軸、Y軸、Z軸 全てをしなくてはなりません X空間だけγ倍したり、時間の刻み方を変換した世界(空間)なんて 現実には(物理として)ありえませんよ(笑) それに X(横・水平)とY(縦・直角)とZ(高さ) これらの空間は「まっすぐ」という概念のもとに成立している いわば線の空間であり XとYとZの間に無限に線の空間が存在します それらは、どうなんだという話になる つまり、ローレンツ変換というのは 無数にある線空間のうちの Xという線空間だけの変換式でしかない 】 それから 真の球面方程式 (二次元のローレンツ変換) において 【 要するに ローレンツ変換は慣性座標系の動く方向と 同じ方向に放射した光に対してのみ使える 一次元の線形変換や! 本来は縦には使えん 縦方向に使いたかったら 二次元のローレンツ変換をせなあかんが じいさんは、そこまでは考えてへん そこでわしは作ったわけです 】 という話をしましたが、このことですね!! 陽天: 球面やとうそぶいとるが、ほんまは直線や マイケルソンとモーリーの実験は ハーフミラーで、水平と垂ちょくに光を分けるから 水平と垂直の2つ方向はええ気がするが x1(y1=0)と、y1(x1=0)の2本の直線やで x1-y1平面ではない 横方向の x1 = C・t1 x1 = -C・t1 縦方向の y1 = C・t1 y1 = -C・t1 の4つの方向のみや それを x1^2+y1^2 = C^2・t1^2 と書いたら あたかもx1-y1平面上の全て方向の光がCになったように錯覚する じいさんの論文中にも x1^2 = C^2×t1^2 (x = C×t) と書いとるがな これが球面(平面)の式のトリックや 皆これに騙されとる x1もy1も軸やない まして空間でもない 平面上の2本の直線や わしは今までくどいぐらい言うてきたはずや 緋山: x1やy1の「1」の意味を教えていただけますか? 陽天: わしがいちいち添字1を付けるんは V1に対する慣性座標系やからで 速度がV2になれば、x2、y2になる くどいようやがもう一度言うと x1は、空間ではなく、空間内(平面上)にある直線や y1は、x1と直交した直線で、x1を90度回転させるとy1になる ローレンツ変換が考慮しとるんはこの2本の直線 (プラスの向きとマイナスの向きの4つのベクトル)だけであって その間の、直線x1とθの角度で傾いたちょく線は考慮しとらん 3次元空間(2次元平面)には、傾きの異なる無限の直線が存在する それを何で2本の直線だけ考慮したら済むんや? 全部の直線で光速をCにせなあかん 緋山: それと本題に入る前にもう1つ ポンチ絵③に、Z軸の式に対して【この式は完全に間違い】とあり ポンチ絵④に、【Zx1は関係ないので Zx1=0 とすると】 とありますが 陽天: Z軸やが、前に言わんかったかな 特殊相対性理論は 慣性座標系が進む方向 (水平の光が進む方向) のX軸のみ特殊で 後の方向は皆いっしょや だから、Y軸もZ軸も違いはない むしろ何のためにY軸とZ軸を分けて2つ作る理由を聞きたい 垂直な軸はY軸だけでことたりる Z軸を考える意味がない 意味がないもんを書くのは無駄ちゅうことです 緋山: イチゼロさんと ヨリノビさんの勘違いから 相対性原理を明かす ② Z軸の定義 ここにつながっていくのですね!! 陽天さん、頭よすぎませんか?(笑) 陽天: 何もようない。普通に考えたらそうなる ローレンツ変換は マイケルソン・モーレィの実験を根拠に発明したもんや だから水平方向(X軸)、垂直方向(Y軸)だけしか考慮しとらんのよ じいさんはローレンツ変換が あたかも三次元空間(実空間)で成り立つように 見せかけたかっただけや みんなそれに騙されとる 緋山: Z軸の定義 において 【 じいさんは、何の前置きもなく 「Z軸方向には光は√(C^2-V^2)で動くと書いとる」と言うたでしょ 詳しく言うと「H軸、Z軸方向には」と書いてあるんやわ それからこれはZ(ゼット)軸やなくてZ(ゼータ)軸や じいさんは何でか知らんがギリシャ文字を使うんが好きでな 論文ではローレンツ変換した後の慣性系の 座標系を(ξ, η, ζ)としとるんや ギリシャ文字は知っとるやろ α、β、γ・・・ 小文字は アルファベットとだいぶ違うから判別できるが ζ(ゼータ)の大文字はZやし η(イータ)の大文字はΗや ξ(グザイ)の大文字はΞだからアルファベットにはない だからじいさんは、Y軸、Z軸のことを言うたんやね 結論は、慣性座標系の進む方向のX軸以外は Y軸(奥行き)とZ軸(高さ)の区別はない 特殊相対性理論は、重力場の話やないんやよ ロケットや光時計をみんな出してくるから 何か重力場の話と勘違いするが X軸にちょっ角な軸は全部同じなんよ たまたま、マイケルソンとモーレイの実験は 重力場でしとるから 地面に沿って地球の進む方向をX軸 地面に沿ってちょっ角方向をY軸 重力の方向と逆向きの方向をZ軸 としただけで 重力を考えないなら、Y軸でもZ軸でも別にかまへん ただ、重力場を考えるならY軸とZ軸を分けて 重力の方向と逆向きにZ軸をとらなあかんよ 】 と言っていましたね!! つまり、アインシュタインは、Z軸はY軸と同じと言いながら ローレンツ変換を出すまで、ずっとZ軸は存在させているわけですね 陽天: じいさんはローレンツ変換後の慣性系の 座標系を(ξ, η, ζ)としていて ζが、わしの表記ではzx1に相当するよ 緋山: さてここからが、今回の本題ですが 陽天さんはこう言っていました 【 じいさんが論文で 「鏡までの距離を0に近づける」ちゅうた意味もわかった 簡単に言うと、球面の方程式は xx1^2 = (Ctx1)^2 これは、xx1 = ±Ctx1 やろ! プラスもマイナスも2乗したら、どっちもプラスや エマン(広江さん)は 「時間軸が始めから逆を向いてしまうことになってしまうから プラスを取るべき」としらっと書いとる 知っとって誤魔化しとるんか知らんで誤魔化しとるんかわからんが 時間軸が逆転するんやない マイナスの場合は光が180度逆向き(-C)なんや それを排除するためにこう言うて誤魔化しとる じいさんは、光が鏡で反射したら逆向くのはわかっとるようや 光が鏡で反射したあとの光の方程式は xx1 = -Ctx1+2M やろ だからじいさんは M(鏡との距離)をゼロに近づけると書いたんやな Mをゼロに近づけると、xx1 = -Ctx1 になる つまり、わからんように 光が鏡を往復する±Cを平均化する操作 〔幾何学でいうと不等辺三角形o1p1q1を ちょっかく二等辺三角形o1pa1qa1 = 光速不変 に変換する平均化変換〕 を入れてあるんや! じいさんは確信犯やが、エマンはわかってないんやろな 】 陽天: わしは、前からじいさんはなんで tx1 = at1+bx1 ・・・ (1) xx1 = dt1+ex1 ・・・ (2) と置いて 2つの点p1→pa1、q1→qa1から 係数をa, b, d, eを求めるわしの方式をとらんと {tx1(0, 0)+tx1(2CM/(C^2-V1^2), 0)}/2 = tx1(M/(C-V1), M) ・・・ (3) から Mを限りなく0に近づける (両軸を原点に近づける)ことで C/(C^2-V1^2)・∂tx1/∂t1 = 1/(C-V1)∂tx1/∂tx1+∂tx1/∂x1 ・・・ (4) などという意味のない偏微分方程式を立てたんかわからなんだ ようやくわかった ちなみに、偏微分係数は線形変換の場合は定数やから 偏微分方程式は単なる線形方程式になる つまり ∂tx1/∂t1 = a ∂tx1/∂x1 = b なので、(4)式は C/(C^2-V1^2)・a = 1/(C-v1)・a+b = 0 ・・・ (4) と同じや tx1=a・t1+b・x1 xx1=d・t1+e・x1 とするなら ∂tx1/∂t1 = a ∂tx1/∂x1 = b ∂xx1/∂t1 = d ∂xx1/∂x1 = e だから、じいさんの作った偏微分方程式など必要ない 何でわしの方式をとらんかったのか? ということになる 緋山: ポンチ絵の②に 【 ただし(5)式を続けて変形して (5)式を移項しただけ】とありますが? 陽天: 書きなぐったメモから、へんなとこがあるな じいさんは(5)式を続けて変形して次の式にしとる ただ、これは(5)式を移項しただけや ちゅう意味や わしが、じいさんに助け船を出したるんも何やが ∂(ax)/∂x = a∂x/∂x だから M(原点と鏡までの距離)も定数だから 前に出して M∂tx1/∂x1+MV1/(C^2-V1^2)×∂tx1/∂t1 = 0 として両辺をMで割ったら 同じ式になるのに、何で回りくどいことをしたんか理解できん そもそも、さっき書いたように 偏微分係数は関数やない。ただの定数a~eや! 緋山: 何で陽天さんの方式をとらなかったのでしょうか? 陽天: おそらくMを0にすることで rox1点と、正しいrx1点を同じ点やと誤魔化す意図がある 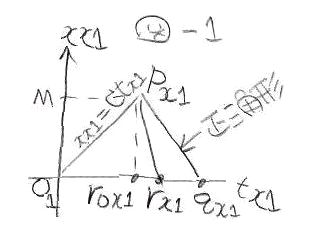 【 前 提 】 ローレンツ変換は 電車とともに移動するBの見る世界の変換です 電車とともに「移動する」と言っても BにとってB(自分)は、つねに距離(xx1)ゼロなので Bは、時間軸(tx1)上を、時間とともに移動していくことになります 鏡はBからつねにМの距離にあります px1点は、Bが01(原点・なおBの原点は時間とともに移動していく) にいたときに、Bのもと(車両の左端)から発射された光が 鏡(車両の右端)にぶつかった位置(tx1,xx1)、つまり(時間,距離)です 距離はМで変わらないので、(tx1,М)です qx1点は、鏡で反射した光がBのもとに戻る位置(tx1,xx1)です BにとってBの距離はゼロなので、(tx1,0)です 三角形が不等三角形=光速不変でない (Bの観測において行く光と戻る光で進む距離は Мで同じなのに、時間が異なる) 正三角形=光速不変である ということになりますが、ここにはトリックがあることは 線形変換の真実 ③ アインシュタインのトリック に書きました 【 しかしや! じいさんの図には誤魔化しがある 時間軸を斜めに取ったように見せかけて 実はr1点だけは、p1点をそのまままっすぐに下した点に取っとるんやよ!! このトリックによって 光速不変にしとる ということです 】 というヵ所を確認してください 緋山: ⑤は、参考書に必ず出てくる球面の式と アインシュタインの導出法とを 並べて書いたものですか? 陽天: そうや 5ページ目は エマンやら皆が使っとる導出法と、じいさんとの比較や だいぶ違うやろ じいさんのはわかりにくいし、偏微分など無駄やから 後世の信者が簡単化したんやろ どっちも間違いやが アインシュタインのはきつねに騙されたようや 間違いがわからんようにしとる 緋山: アインシュタインの方も 結局、球面の式を使うわけですね!! 陽天: そうや じいさんも同じ球面の式を使う 両者とも球面の式 xx1^2 = C^2・tx1^2 を使って 実はその解が xx1 = C・tx1 と xx1 = -C・tx1 となるんを 2乗したまま誤魔化しとるんや マイケルソンとモーリーの実験のみ 縦と横の往復の2方向 (縦と横のプラスマイナスの4方向)に出とるといえるが xx1^2+yx1^2 = C^2・tx1^2 ではない xx1 = C・tx1 xx1 = -C・tx1 yx1 = C・tx1 yx1 = -C・tx1 の4つの式に分けなあかんがな 全ての方向をいっぺんに変換する? じいさん、アホなこと言わんでくれ 緋山: ⑤に、球面方程式の(2)式に矛盾するとありますが 陽天: 2つの式を見比べてみ xx1^2+yx1^2 = C^2×tx1^2 【エマンの球面の式】 xx1^2 = C^2×tx1^2 (xx1 = C×tx1) 【じいさんの球面の式】 が、両方とも成立するんは yx1 = 0 しかない また x1^2+y1^2+z1^2 = C^2×t1^2 と書くから騙される 同様に、じいさんも論文中の x1^2=C^2×t1^2 と 両式が成立するんは y1^2=0 z1^2=0 つまり、y1=0 z1=0 以外にはない 緋山: 結局、yも、zも、ゼロになる zx1^2 = 0 つまり z = 0 になるのですね 陽天: 要するに、球面の式は異なる方向(ベクトル)の光を 一個ずつ式にせんと意味がないちゅうことや 陽天: わしが言うとる最重要な点を忘れたらあかんで じいさんの式 xx1^2+yx1^2 = C^2×tx1^2 ・・・ (1) は円の式とされておるけど ここがトリックやちゅうたやろ もう一度、2つの式を見比べてみ xx1^2+yx1^2 = C^2×tx1^2 (エマンの球面の式) xx1^2 = C^2×tx1^2 (じいさんの球面の式) が、両方とも成立するんは yx1 = 0 しかない と言ったが yx1についてもそや xx1^2+yx1^2 = C^2×tx1^2 (エマンの球面の式) yx1^2 = C^2×tx1^2 (じいさんの球面の式) が両方とも成立するんは xx1 = 0 しかない つまり (1)で有効なんは xx1^2 = C^2・tx1^2 → xx1 = ±C・tx1 と yx1^2 = C^2・tx1^2 → yx1 = ±C・tx1 だけや 式(1)で、考慮しとる点は 円が、xx1軸とyx1軸と交わる4点で 円周の全ての点やない ここが最大のトリックや 世の中には 特殊相対性理論のトリックを論じている人も 肝心のここのトリックには気が付いとらん エマンに至っては、4×4行列 (a1, a2, a3, a4) (a5, a6, a7, a8) (a9, a10,a11,a12) (a13,a14,a15,a16) を2×2行列 (a1, a2) (a3, a4) にする無駄な変形をガタガタし 「一言言わせてくれ わしがガタガタ変形したんは 特殊相対性理論を間違いやという奴らに 付け込む隙を与えんためや」ちゅうとる 緋山: 電車とともに移動するBさんと 鏡の距離(М)は変わらないですよね いったいどうやって アインシュタインは 鏡の距離を限りなく0にしたのですか? 陽天: 算数的に言うと Mはx1軸上の任意の定数であって、変数ではないやが それに微分を持ち込んで、変数(関数)としたんやね 手書きの②ページのMを限りなく 0に近づけるちゅうんは微分の基本的な発想や limf(x+Δx)/Δx → f'(x) Δx → 0 f'(x)を、f(x)の微分または導関数というよ 緋山: アインシュタインが 意味のない偏微分方程式を使ったのは 【 M'を0にすることで rox1点と、正しいrx1点を同じ点やと誤魔化す意図がある】 と言っていましたが 具体的にはどういうことですか? Bさんと鏡の距離(М)が微分を持ち込むことで 変わるというのがよくわかりません 陽天: 直角二等辺三角形を無限に小さくすると rox1とrx1が近づくわけや しかし虫メガネで見たら、やっぱりrox1とrx1は別の点やで!!  陽天: 清書しといたで!! |
|