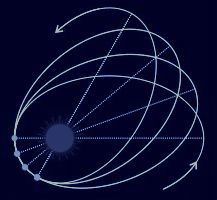
EMANの物理学のHさん 顔洗って出直してくれ!!② 水星の近日点による一般相対の証明 EMANの物理学 というサイトを運営している 広江克彦さん という人がこんなこと言っています https://eman-physics.net/relativity/mercury.html (水星の近日点移動) 世の中には相対論が完全に間違っていると考えている人がいて, 仲間を増やそうと大々的に宣伝を行っているのを良く見かける. しかしそういう人たちは,相対論に代わって この数値を説明できるだけの代案を示さなくてはならないことになる. それは非常に難しい事だろうし, 無駄な努力に終わる可能性の方が高いだろう. それに賭けたのならば, 人生を捨てる覚悟で相当頑張ってもらわないといけない. いや,彼らが頑張っているのは知っている. しかし相対論に反対するキャンペーンの方ばかり頑張ってもらっても, 人生を棒に振る人が増えてしまってとても心配になるのだ. 私のところにもそういうロビイストたちがコンタクトを取ろうとしてくる. 「間違った理論に騙されている私」を救おうとして,熱心に説いてくる. その気持ちは本物だが, 彼らの説く内容は幼稚で穴だらけ,矛盾だらけである. 私がその不備や勉強不足を指摘しても, 彼らは私の頑なさに失望し,私のことを憐れみながら去って行くのである. 私もまた彼らを憐れんでいる. 彼らが自身の勉強不足を棚に上げて, 自分こそは正しいと信じ切っている高慢さに. 【 お願い事 当サイトへのリンクはどの記事に対してもご自由にどうぞ。 お問い合わせの必要はありません。 ただし記事の部分的な引用をする場合には、 併せて元記事へのリンクを設けるか あるいはその記事のURLを明記して下さるようお願いします。 なぜなら、全体の文脈を無視した、 誤解を与える引用が時々目に付いて 世間様に申し訳なく思えることがあるからです。 】 惑星は、太陽の引力によって太陽の周りを回っているため 惑星が受ける太陽の引力が分かれば、軌道が計算で導き出せる ということになります そして、実際の観測で分かっていた惑星の軌道を比べてみると 完全に符号したので 「万有引力の法則」は、絶対的な真理となったそうです 但し、万有引力の軌道計算に対して 水星の軌道がごくわずかズレるという問題が残っていたのです 一般相対性理論と、万有引力では ほぼ同じ、惑星の軌道計算が導き出されます 但し、水星だけは、違ってきます アインシュタインによると 理由は、水星が太陽に一番近い惑星であり 太陽の重力によって、時空がゆがみ 水星の軌道に、わずなズレが生じるからである ということです そして一般相対性理論の式によると このズレが解決できるため これによって 万有引力の法則は、重力の強い場所では使えないことが分かった という話が「水星の近日点移動に関する問題」です 惑星が、太陽に最も近くなる位置を「近日点」と呼びますが 水星の近日点は、移動していくことが観測から分かっていました これは、水星の楕円の軌道が 下の図のように少しずつにズレていくことから起きる とされています
ズレの原因のほとんどは 他の惑星からの重力の影響として 万有引力の数式で説明できるそうですが それでも100年で、574秒ズレるうちの 43秒のズレの説明がつかなかったのです 〔ここでいう秒は、時間でなく角度の単位で 1度の 1/60 が 1分、その 1/60 が 1 秒〕 この水星の近日点の移動は GPS衛星の時間の遅れ などとともに 一般相対性理論の正しさを証明する 重要な根拠の1つになっています 100年で、574秒しかズレない こう聞くと、一般の人は、宇宙物理学って めちゃめちゃ正確でものすごい世界のように 騙されてしまいますが、大嘘!! 冥王星の質量の推移は 以下のとおりです 数字は地球質量(地球を1とした場合の質量) 1915年 7 (未発見の惑星Xとしての質量) 1931年 1 1948年 0.1 1976年 0.01 1978年 0.0015 2006年 0.00218 (=1/500) 以上、ウィキペディアより かつては(1931年までは) 冥王星の質量は、地球の7倍、いまでは1/500倍じゃないですか(笑)
アインシュタインが 一般相対性理論を発表したのは1915年ですよ 冥王星の質量の推移は 一般相対性理論の解のデタラメさを如実に示しています 水星の近日点に関しては 杉岡幹生先生の21世紀物理学の新しい公理の提案 http://www5b.biglobe.ne.jp/~sugi_m/page264.htm というサイトに 素敵な考察があります かいつまんで書くと以下のとおりです 【 太陽からは、猛烈な風が吹いている 太陽風は、強烈な超高速のプラズマ大気の流れであり 太陽系の果てまでも吹いている 彗星に、尾っぽを常に太陽と反対方向へ向けさせるほどの強い風である 水星は太陽に最も近く、月よりほんのわずか大きいだけの星である 太陽風の影響を受けないわけがない また、水星の軌道は楕円である 仮に軌道が円で、太陽風の強さが一定なら 太陽風が水星の軌道に与える影響は少ないが 軌道が楕円であるとなると、水星が受ける太陽風の強さは一定でない しかも、太陽風の強さは、太陽の黒点の周期とも関係し 11年周期で変動しているという報告もある 太陽風は電荷を帯びたプラズマの流れのようなので 水星が磁場をもっていればさらに 太陽風による影響は大きいだろうと予想されるが 水星も磁気圏をもっているようである まだまだ太陽系はわからないことだらけで 色々と発見が続いている いずれにせよ 一般相対論による水星の近日点移動計算がなされた 20世紀前半では、太陽風があるなどとはみな思ってもみなかった 天文学が発達した現在、当然、当時の計算は正しかったのか? という疑問をもち 太陽風というパラメータを入れて、計算をし直さなければならない ところが、不思議なことに 「水星の近日点移動は、ニュートンの理論では合わないが 一般相対論を使って計算すれば観測値とピタリと一致した」と称賛し 水星の近日点移動への疑問は 「触れてはいけない!」と言わんばかりの態度をとっている これは科学としての態度ではない 】 アインシュタインのトリックがわかった! 100年分の目からウロコ https://woorex.com/02_soutai/02_04_01.html というサイトを運営されている 日高まもる先生は 相対性理論というのは 古典物理学では一致しない実験値との差を 関数を導入することで 一致させることを目的として始めた理論なのだから 実験値と計算が一致するのはあたりまえ とおっしゃられています 緋山: 原子や分子の世界では 支配的なのは重力ではなく電磁気力です マイナスの電子と プラスの原子核内の陽子との間に働く電磁気力の引力が 重力が、地球に太陽を周りを回らせているのと同じように 電子に原子核のまわりを回らせています ただ、物体はプラス電荷とマイナスの電荷を ほぼ同数含んでいるので、引力と斥力が、ほぼ打ち消されてしまい 太陽や地球のような大きな世界では 電磁気力は非常に小さくなるといいます これに対して、重力は、ごく弱い力なので 素粒子や原子の世界を説明するときには その効果はふつう無視できるそうです ところが、重力には斥力がなくつねに引力だけなので 重力の効果は、すべて積み上げられていく なので十分な数の物質粒子が存在すれば 重力は他の力を圧倒することができるというのです 恒星程度の大きさになると、重力は、他のすべての力にうち勝って 星を崩壊させることができるといいます また、重力は太陽と地球といったような長距離まで作用を及ぼす このため重力こそが宇宙の進化を決定しているといいます 冥王星が太陽系の惑星から外された理由は 1、質量は、地球の衛星である月の0.2倍以下であり 太陽には冥王星より質量が大きい衛星が7つもあることが分かった 2、冥王星に似た天体が数多く発見され、その数は1000を超えている 3、2003年に冥王星の近くに冥王星よりも大きな 天体「エリス」が発見された とされています 【冥王星に似た天体が数多く発見され、その数は1000を超えている】 といった天体の重力を無視して 正しい惑星の軌道を計算できるのでしょうか? 陽天: 水、金、地、火、木、土、天、海と あらゆる小惑星を全部連立させて 微分方程式を解くのはスパコンでも無理や 今は、小さな星の重力を無視(微小な摂動)して 惑星の軌道を計算しとる わしが驚くのは地球の動きの正確さや とはいえ地球が一年と1/4日で 厳密に同じ位置に来とるかどうかも証明できん 昔からの概念でしかない 誰も証明してへん 第一、太陽系は銀河の周りを高速で回っとることがわかっとる 太陽座標系では同じ位置でも、銀河座標系では同じ位置やない ずっと離れとる 【 国立天文台によると 太陽系と天の川銀河の中心までの距離は 約26,100光年、太陽の移動速度は秒速約240km
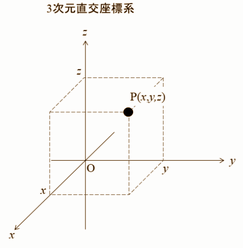
太陽系の公転周期(天の川銀河の中心を1周)は 約2億2,000~2億5,000万年とされていて 太陽系が生成されてから、まだ20~25回くらいしか周回していないそうです さらに、天の川銀河(銀河系)も 膨張する宇宙に乗るかたちで 秒速約630km(時速約216万km)の速度で移動しているそうです つまり、太陽系の惑星は、静止した太陽の周囲を回っている のではなく 惑星は、太陽とともに高速で移動しつつ 惑星からみて、静止している太陽の周りを回っているわけです 】 陽天: わしら人類はどんどん新しい知識を得る だから科学は進歩する それが、相対性理論だけは1915年から止まったままや じいさんは太陽も金星も丸い球やとして計算しとるが 今では、太陽も金星も回転楕円体やとわかっとるし 質量も当時よりずっと正確にわかっとる 銀河系も高速で移動しとるのもわかってきた 水星の近日点については じいさんが、ぴったり合うように鉛筆舐めたに決まっとる そもそも、水星の近日点移動はたったの575秒=0.0266度や 他の惑星からの引力の効果で、0.0246度までは計算ができとる じいさんは、残りの0.002度の差を 一般相対性理論で証明したというたんやで 絶対値も小さいし、観測値は万有引力の計測値の7.5%や これを大きいと見るか小さいと見るかは人によるが わしは誤差の範囲やと思うとる 誤差は、太陽系全体が 天の河銀河を回る運動と関係しとるかもしれん 緋山: 当時のデータをもと 水星の近日点をぴったり合うように鉛筆舐めたとしても 今はどうなんだ という話になりますよ(笑) 仮に、水星の近日点の計算が 今も当時と変わらずに正しいかったとしても では、冥王星の質量はどうなんだ という話になる(笑) 日高先生によると 相対論の立証例は一致した時点のデータを いつまでも繰り返し引用する傾向がある 相対性理論を証明するには 時間と空間が歪んでいるという直接的な証拠以外にない とした上で 古典力学的な実験装置で 時空の歪みなど測定できるものではない 実験値の差を数学的に埋めたとしても それにより時空の歪みが証明されたことにはならない 古典力学的な実験装置で観測したデータを 相対論で補正することが、そもそも数学的に誤りである なので、最新の検証がどこまで詳細に 実施されたものであるかはさほど問題ではない (たとえ一般相対と一致したとしても、時空の歪みの証明にはならない) とのことです この話はとても重要なので 私が補足させていただきます 数学とは、世界を数で定義する学問と言えますか? という質問を、知り合いのアルゴリズムの教授にしてみました 【 例えば、0より小さい数が考えられるようになり 「今日は、昨日よりも気温がマイナス2℃だった」 という表現が可能になった という意味は 水の氷る温度を0℃と決めて 負の数を用いることで、温度(熱)という世界を定義していますよね すると、数学とは、一種の自然科学と 言えなくもなさそうですが 数学には、単に、数学自身を 研究対象とされている場合もありますか? 】 と質問したわけです 教授の答えはこうです 現代数学は数学自身が研究対象で、それ以外の動機はないと思います 但し、そういった「何の役にも立たない」はずの数学が 「後になって」何かの現象を説明することはよくあります それから、高校までで扱っている数学については おそらく全て他分野の必要で出てきたもので 色んな現象を説明するための道具だったのは間違いありません ですので、割と最近まで自然科学の一分野だったはずです (あくまで私の認識ですが) 緋山: ウィキペディアで調べてみると 現代数学の父 ヒルベルト(1862~1943・ドイツの数学者)は 【 数学は決められたルール (公理と推論法則)に従って行われるゲームであり ルールを取り替えることによってできる異なるゲームは それぞれ同等である 】 と述べています つまり、大学から勉強する数学は あるルールのもとになされるゲームにすぎず ゲームに真理も虚偽もないのと一緒で 現代数学の数式が、現実世界の真理を表わしている わけではないということです 教授によると ① 公理(定義)と、推論規則を厳密に定めて 議論する方向にシフトした ② これにより数学内で モデルを構築して議論をすることが可能となった ③ モデルが現実にないものであったとしても 公理(定義)と推論規則が整えばそれでモデルになる ④ こうして自然科学から離れた数学独自の問題を 扱えるようになった これが現代数学ということです 緋山: 3次元空間の直交座標系は、空間内で 互いに直交する3本の数直線 x軸、 y軸、z軸を 決めることによって定められます
(y軸、z軸は、平面上にあり、x軸は、平面から手前に出ています イメージ的には、紙の上から斜めにペンが手前に出ているような感じ) しかし、4次元の座標というのは存在していません つまり、誰も描くことができません にも関わらず 数学では、4次元、5次元・・・・ n次元 も表わせるといいます これについても簡単に説明してもらえますか? と、教授に聞いてみました 教授: 我々のいる世界では (実際に何次元で構成されているかはともかく) 人間は、3次元までしか認識できないわけですが ベクトルの成分の個数を増やしてあげれば 何次元でも表現できて、【数学の上】では n次元空間を表現することができます 「n次元なんて実際にあるのか?」という質問は 数学では愚問で、モデルとして成立する(矛盾しない) ならば存在すると考えるのが数学です 数学はあくまで数学の中という 閉じた世界で、理論を組み立てているので 物理とか、他のところで使えるかはどうでもいい話なのです とのことです つまり、日高先生の主張は 古典物理学の実験装置での誤差は あくまで三次元世界の話であり その誤差を新しい理論が主張する ≪時空≫などというわけの分からない概念を持ちだしてきて 埋めようすること自体 「数学を物理へ応用する」という観点から間違っている ということなのです 現実世界にゲームの論理をもちこんで 証明もへったくりもないということです だいたい「相対性理論は正しい」の根拠となっているのは 水星の近日点 の他は GPS衛星、ミューオン粒子、日食による重力レンズ 重力波ぐらいなもので これらはどれもデタラメで、そのトリックはあまりに幼稚です 【はじめに】で書いたように あたりまえの話ですが ≪9の事例で相対性理論が正しいから、1の事例で間違えだったとしても 相対性理論は崩壊していない≫なんて話は通用しません 「帰納証明」というのは1つでも間違った事例が出たら それでもうお終いなのです それに私から言わせると なに一つ相対性理論において 証明されている実証例なんてありませんよ(笑) ついでに、星の質量なんてどうやって計算してるのか? という疑問に答えておきましょう ニュートン(1642~1727)が「万有引力の法則」を発見し 万有引力の数式から 潮の満ち引きなど、多くの自然現象が説明できるようになりました 実際の観測で分かっていた惑星の軌道とも 完全に符号したので 「万有引力の法則」は、絶対的な真理となったわけです ところが、ニュートンの「万有引力」発見の約100年後 天王星(てんのうせい)がみつかり この天王星についての軌道が 実際の観測結果と、万有引力の計算式の結果とが一致しない という事態が生じます この問題については 天文学者 ユルバン・ルヴェリエ(1811~77)が 天王星の近くに未知の天体があることを予言し 未知の惑星(海王星)が発見されたことで解決に至りました こうして「万有引力の法則」の真理性は保たれましたが 小さな問題が1つ残っていました それは、万有引力の軌道計算に対して 水星の軌道がごくわずかズレることでした これが「水星の近日点移動の問題」です さて、天王星の軌道が 海王星に乱されていたのと同じように 冥王星の発見は、海王星の軌道も 未発見の惑星(惑星X=冥王星)によって乱されている との予言を発端とします 太陽と地球の2つの星しかなければ 地球はきれいな楕円軌道を描きますが そこに木星があると木星に引っ張られます しかも、木星の位置に応じて 軌道の外側に引っ張られたり、内側に引っ張られたりします ◎木星 ●地球 ◯太陽 という位置だと 地球は通常の軌道より外側に引っ張られるし (太陽と木星で地球を逆方向に引っ張り合う) ●地球 ◯太陽 ◎木星 という位置だと地球は通常の軌道より 内側に引っ張られます (太陽と木星が同じ方向に引っ張る) 太陽ほどではなくても 木星から少し引っ張られるので 地球、太陽、木星の位置関係で 地球にかかる力が変わってきます 要はそういう他の天体への影響を観測して それを状況証拠に惑星があるだろうと 予想を立てているわけです 実際、冥王星も予想が先になされて それから発見されました そのときの質量が地球の7倍です 1931年に、地球と同じ(1倍)になるまで変更されていません 現在 、地球の1/500ですから(笑) 冥王星の近くに冥王星よりも大きな 天体「エリス」が発見された 当時はエリスを計算に入れていなかった としても 7倍が1/500倍であったなんてデタラメすぎです つまり、人類は、太陽系のことですら おおざっぱなことしか分からないのです それでいて一般相対が「真理」(・_・?) だってもへちまもありませんよ ということなのです 陽天: 物理学は、宇宙を方程式で記述する学問やが その方程式は、微分方程式やから 「物理学とは微分方程式を作り、それを解く学問である」 と言うても差支えない しかし、ほとんどの微分方程式は、解析的に解くことはできん 解析的に解くとは、微分方程式を積分して その微分方程式が満足する関数 (原始関数と呼ぶ)を求める解き方のことです また、複雑でかつ連立した微分方程式は手では解けないから コンピュータを使って解く これをコンピュータシミュレーションと言う 但し、コンピュータで解けるのは、解析解ではなく数値解やで 数値解とは、原始関数を求めるのではなく 数値として近似的に解くことや しかも空間上のある一点だけの解を求めるものや 初期条件やパラメータ(変数)を動かしたら、解がどうなるかは 計算してみないと分からん これに対して解析解は、原始関数が求まるので 変数の変動に対して、解がどういう挙動=振る舞い を示していくのかを知れる その原始関数から、その値がどういう挙動=振る舞い を示していくのかをある程度予測することができる 例えば10mの枝からりんごが何秒後に地面に落ちるかは 計算をしなくとも原始関数からわかる しかし、現実には原始関数は惑星の運動ぐらいしか求まらへん 船のマストから、石を落とす運動を計算する場合 方程式が1個ならええが、実際はたくさんいる 当然、空気抵抗があるし 突風が石の軌道を曲げるかもしれん 世の中にはランダムな外乱があり 現実には、解析解(原始関数)は存在しないといってもいい 相対性理論信者こそ高慢や 理論が合うとるか間違っとるかに高慢は関係やない 間違っとることを証明したらええだけや EMANの物理学のHさん 顔洗って出直してくれ!!③ EMANの物理学のHさん 顔洗って出直してくれ!!① (ひとつ戻る) |
|